Basic Math: Geometric Mean Average

The geometric mean is the average of a set of numbers by using the product of their values, as opposed to using the sum, as in the arithmetic mean. The value of this method of calculating average can be seen commonly when calculating the performance of an investment or portfolio.

Technically, it is “the nth root product of n numbers.”

Generally speaking, you use the geometric mean when working with percentages, while using standard arithmetic mean when working with individual values.

One of the biggest reasons to use this method of “averaging” when looking at portfolio performance is that it considers the effects of compounding. Simply using the arithmetic mean will not provide your correct performance numbers. 

The geometric mean is also called the compounded annual growth rate or time-weighted rate of return.

Geometric Mean Formula
μ geometric =[(1+R₁ )(1+R₂ )…(1+R_n )]^1/n −1
where: R₁ …R_n are the returns of an asset (or other observations for averaging).

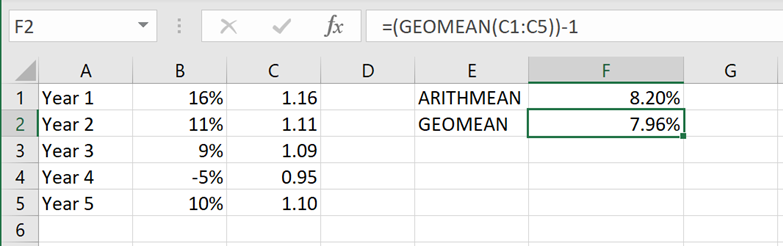
Geometric Mean Example:
Suppose you have a $1,000 investment that pays 10% every year for 30 years on the balance in the account at the end of the year. In other words, the investor is getting paid interest on the interest – also known as “Compound Interest.”

Year 1 Interest = $100    ($1,000 x 10%)                New Principal amount = $1,100
Year 2 Interest = $100    ($1,100 x 10%)

In this case

calculate the interest in year one, which is $10,000 multiplied by 10%, or $1,000. In year two, the new principal amount is $11,000, and 10% of $11,000 is $1,100. The new principal amount is now $11,000 plus $1,100, or $12,100.

In year three, the new principal amount is $12,100, and 10% of $12,100 is $1,210. At the end of 25 years, the $10,000 turns into $108,347.06, which is $98,347.05 more than the original investment. The shortcut is to multiply the current principal by one plus the interest rate, and then raise the factor to the number of years compounded. The calculation is $10,000 × (1+0.1) 25 = $108,347.06.

For example, the geometric mean calculation can be easily understood with simple numbers, such as 2 and 8. If you multiply 2 and 8, then take the square root (the ½ power since there are only 2 numbers), the answer is 4. However, when there are many numbers, it is more difficult to calculate unless a calculator or computer program is used.

The longer the time horizon, the more critical compounding becomes and the more appropriate the use of geometric mean.

The main benefit of using the geometric mean is the actual amounts invested do not need to be known; the calculation focuses entirely on the return figures themselves and presents an “apples-to-apples” comparison when looking at two investment options over more than one time period. Geometric means will always be slightly smaller than the arithmetic mean, which is a simple average.

Key Takeaways

• The geometric mean is the average rate of return of a set of values calculated using the products of the terms.
• It is most appropriate for series that exhibit serial correlation. This is especially true for investment portfolios.
• Most returns in finance are correlated, including yields on bonds, stock returns, and market risk premiums.
• For volatile numbers, the geometric average provides a far more accurate measurement of the true return by taking into account year-over-year compounding that smooths the average.

Excel Syntax
=GEOMEAN (number1, [number2], …)

Arguments
number1 – First value or reference.
number2 – [optional] Second value or reference.

Example of Geometric Mean

If you have $10,000 and get paid 10% interest on that $10,000 every year for 25 years, the amount of interest is $1,000 every year for 25 years, or $25,000. However, this does not take the interest into consideration. That is, the calculation assumes you only get paid interest on the original $10,000, not the $1,000 added to it every year. If the investor gets paid interest on the interest, it is referred to as compounding interest, which is calculated using the geometric mean.

Using the geometric mean allows analysts to calculate the return on an investment that gets paid interest on interest. This is one reason portfolio managers advise clients to reinvest dividends and earnings.

The geometric mean is also used for present value and future value cash flow formulas. The geometric mean return is specifically used for investments that offer a compounding return. Going back to the example above, instead of only making $25,000 on a simple interest investment, the investor makes $108,347.06 on a compounding interest investment. Simple interest or return is represented by the arithmetic mean, while compounding interest or return is represented by the geometric mean.

Arithmetic Versus Geometric Mean

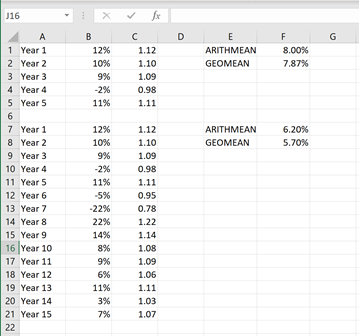
Look. Do you HAVE to use this? Of course not. I think it’s a great tool to compare against the ‘regular’ mean average. As you can see from the examples above, the geometric mean is sufficiently different to matter when you are looking at performance of an investment. Just another tool in the toolbox!